我在 2016 年的时候写过一篇关于 向量的叉乘与行列式的文章,没想到过去这么久了广大网友呼声还这么高,基于很多大学生的需求,我决定帮你们啃下难啃的高数和线性代数,让你们从根本上理解这两门课,而不是只知道背公式。到时候别忘了给我发红包哦~~~
今天我们来讲讲矩阵的乘法。当然了,我告诉你的肯定不是大学教科书上那些填鸭式的云里雾里的计算规则,你可能将规则背下来了,但完全不理解为什么会这样。别怕,我将会在这篇文章中为你带来矩阵乘法的全新体验。
先来回顾一下矩阵加法,还蛮简单的,就是相同位置的数字加一下。
$$\begin{bmatrix} 2 & 1 \\ 4 & 3 \end{bmatrix} + \begin{bmatrix} 1 & 2 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} 3 & 3 \\ 5 & 3 \end{bmatrix}$$
矩阵乘以一个常数,就是所有位置都乘以这个数。
$$2 \cdot \begin{bmatrix} 2 & 1 \\ 4 & 3 \end{bmatrix} = \begin{bmatrix} 4 & 2 \\ 8 & 6 \end{bmatrix}$$
但是,等到矩阵乘以矩阵的时候,一切就不一样了。
$$\begin{bmatrix} 2 & 1 \\ 4 & 3 \end{bmatrix} \cdot \begin{bmatrix} 1 & 2 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} 3 & 4 \\ 7 & 8 \end{bmatrix}$$
这个结果是怎么计算出来的呢?大多数人知道的计算方法应该是教科书上给出的,我们就先来看这种方法。
教科书告诉你,计算规则是,第一个矩阵第一行的每个数字(2和1),各自乘以第二个矩阵第一列对应位置的数字(1和1),然后将乘积相加( 2 x 1 + 1 x 1),得到结果矩阵左上角的那个值3。
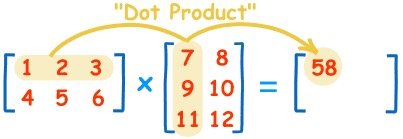
也就是说,结果矩阵第 m 行与第 n 列交叉位置的那个值,等于第一个矩阵第 m 行与第二个矩阵第 n 列,对应位置的每个值的乘积之和。
假设 $$A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}$$
$$B = \begin{bmatrix} b_{11} & b_{12} & \cdots & b_{1p} \\ b_{21} & b_{22} & \cdots & b_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ b_{n1} & b_{n2} & \cdots & b_{np} \end{bmatrix}$$
令
$$C = A \cdot B$$
其中,$C = \begin{bmatrix} c_{11} & c_{12} & \cdots & c_{1p} \\ c_{21} & c_{22} & \cdots & c_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ c_{m1} & c_{m2} & \cdots & c_{mp} \end{bmatrix}$
可以得出矩阵 $C$ 每个元素的表达式为
$$C_{ij} = a_{i1} \cdot b_{1j} + a_{i2} \cdot b_{2j} + \cdots + a_{in} \cdot b_{nj} = \sum_{k=0}^{k=n} a_{ik} \cdot b_{kj}$$
这就是矩阵乘法的一般性法则,人们一般都用这个法则来计算,我也不例外。不过我觉得还是有必要讲讲其他几种方法,比如考虑整行或整列。下面还是继续拿矩阵 $A$ 和 $B$ 举例。
列向量视角#
先将矩阵 $A$ 和 $B$ 的每一列看成一个向量,例如:
$$\vec{a_1} = \begin{bmatrix} a_{11} \\ a_{21} \\ a_{31} \\ \vdots \\ a_{m1} \end{bmatrix}$$
$$\vec{b_1} = \begin{bmatrix} b_{11} \\ b_{21} \\ b_{31} \\ \vdots \\ a_{n1} \end{bmatrix}$$
这样就可以把矩阵 $A$ 和 $B$ 写成如下的形式:
$$A = \begin{bmatrix} \vec{a_1} & \vec{a_2} & \vec{a_3} & \cdots & \vec{a_n} \end{bmatrix}$$
$$B = \begin{bmatrix} \vec{b_1} & \vec{b_2} & \vec{b_3} & \cdots & \vec{b_p} \end{bmatrix}$$
现在如果我将矩阵 $A$ 和向量 $\vec{b_1}$ 相乘会得到什么?通过前面的一般性法则我们知道大小为 m x n 的矩阵乘以大小为 n x p 的矩阵得到的矩阵大小为 m x p。
我们来耍一些小聪明,让矩阵 $A$ 以列向量 $\vec{a_i}$ 作为其元素,而矩阵 $\vec{b_1}$ 以 $b_{j1}$ 作为其元素。这样看来,矩阵 $A$ 的大小为 1 x n,矩阵 $\vec{b_1}$ 的大小为 n x 1,所以 $A \cdot \vec{b_1}$ 的大小为 1 x 1,这也是一个列向量。如果你代入上面的一般性法则,可以发现 $A \cdot \vec{b_1}$ 恰恰就是矩阵 $C$ 的第一列。同样,如果把矩阵 $C$ 的每一列看成一个向量,那么
$$A \cdot \vec{b_1} = \vec{c_1}$$
其中,$\vec{c_1} = \begin{bmatrix} c_{11} \\ c_{21} \\ c_{31} \\ \vdots \\ c_{m1} \end{bmatrix} = \vec{a_1} \cdot b_{11} + \vec{a_2} \cdot b_{21} + \vec{a_3} \cdot b_{31} + \cdots + \vec{a_n} \cdot b_{n1}$
发现了什么?$\vec{c_1}$ 其实就是矩阵 $A$ 中所有列的线性组合!
更一般性地,我们可以推出:
$$\vec{c_i} = A \cdot \vec{b_i} = \vec{a_1} \cdot b_{1i} + \vec{a_2} \cdot b_{2i} + \vec{a_3} \cdot b_{3i} + \cdots + \vec{a_n} \cdot b_{ni}$$
至此我们得到了一个优美的结论:
到这里你应该能领悟为什么矩阵 $C$ 的行数与矩阵 $A$ 的行数相同了,也就是矩阵 $C$ 的列向量与矩阵 $A$ 的列向量大小相同。
怎么样,是不是有一种茅塞顿开的感觉?别急,下面我们再换一种理解角度。
行向量视角#
先将矩阵 $A$ 和 $B$ 的每一行看成一个向量,例如:
$$\vec{a_1} = \begin{bmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \end{bmatrix}$$
$$\vec{b_1} = \begin{bmatrix} b_{11} & b_{12} & b_{13} & \cdots & b_{1p} \end{bmatrix}$$
这样就可以把矩阵 $A$ 和 $B$ 写成如下的形式:
$$A = \begin{bmatrix} \vec{a_1} \\ \vec{a_2} \\ \vec{a_3} \\ \vdots \\ \vec{a_m} \end{bmatrix}$$
$$B = \begin{bmatrix} \vec{b_1} \\ \vec{b_2} \\ \vec{b_3} \\ \vdots \\ \vec{b_n} \end{bmatrix}$$
同理,你会发现 $\vec{a_1} \cdot B$ 恰好就等于矩阵 $C$ 的第一行。同样,如果把矩阵 $C$ 的每一行看成一个向量,那么
$$\vec{a_1} \cdot B = \vec{c_1}$$
其中,$\vec{c_1} = \begin{bmatrix} c_{11} & c_{12} & c_{13} & \cdots & c_{1p} \end{bmatrix} = a_{11} \cdot \vec{b_1} + a_{12} \cdot \vec{b_2} + \cdots + a_{1n} \cdot \vec{b_n}$
更一般性地,我们可以推出:
$$\vec{c_j} = \vec{a_j} \cdot B = a_{j1} \cdot \vec{b_1} + a_{j2} \cdot \vec{b_2} + \cdots + a_{jn} \cdot \vec{b_n}$$
又得到了一个结论:
现在你应该能领悟为什么矩阵 $C$ 的列数与矩阵 $B$ 的列数相同了,也就是矩阵 $C$ 的行向量与矩阵 $B$ 的行向量大小相同。
故事到这里就结束了吗?远远没有,下面我们再换一种理解角度。
鬼畜视角#
常规性的一般性法则其实是拿矩阵 $A$ 的每一行去乘矩阵 $B$ 的每一列的。现在我们反过来思考一下,如果拿矩阵 $A$ 的每一列去乘矩阵 $B$ 的每一行会发生什么?
为了方便计算,我们将矩阵 $A$ 的每一列看成一个向量,而将矩阵 $B$ 的每一行看成一个向量,即:
$$\vec{a_i} = \begin{bmatrix} a_{1i} \\ a_{2i} \\ a_{3i} \\ \vdots \\ a_{mi} \end{bmatrix}$$
$$\vec{b_i} = \begin{bmatrix} b_{i1} & b_{i2} & b_{i3} & \cdots & b_{ip} \end{bmatrix}$$
矩阵 $\vec{a_i}$ 的大小为 m x 1,矩阵 $\vec{b_i}$ 的大小为 1 x n,发现了什么?$\vec{a_i} \cdot \vec{b_i}$ 得到的是一个大小为 m x n 的矩阵!等等,矩阵 $C$ 的大小不也是 m x n 吗?没错,就是这么神奇,事实上矩阵 $C$ 等于矩阵 $A$ 的每一列与矩阵 $B$ 每一行的乘积之和。下面省略一万字的证明,直接给出公式:
$$C = \vec{a_1} \cdot \vec{b_1} + \vec{a_2} \cdot \vec{b_2} + \cdots + \vec{a_n} \cdot \vec{b_n}$$
结论:
举个例子,设矩阵 $A = \begin{bmatrix} 2 & 7 \\ 3 & 8 \\ 4 & 9 \end{bmatrix}$,矩阵 $B = \begin{bmatrix} 1 & 6 \\ 0 & 0 \end{bmatrix}$,那么:
$$A \cdot B = \begin{bmatrix} 2 \\ 3 \\ 4 \end{bmatrix} \cdot \begin{bmatrix} 1 & 6 \end{bmatrix} + \begin{bmatrix} 7 \\ 8 \\ 9 \end{bmatrix} \cdot \begin{bmatrix} 0 & 0 \end{bmatrix}$$
你有没有发现,你每切换一次视角,你就会对矩阵乘法理解的更深刻。事实上世间万物皆是如此,这里我顺便谈一下”理解“和”理解“的本质,因为理解是我们每个人的目标,我们想要去理解事物。我认为理解和切换视角的能力密切相关,如果你没有切换视角的能力,你就无法理解事物。关于数学,很多人认为数学就是加减乘除、分数、几何代数之类的东西,但实际上数学和模式密切相关,每切换一次视角,你就会得到一种全新的模式。我所说的模式是指影响我们观察的关系、结构以及规律。
当然了,关于矩阵的乘法还有很多种理解方式,你可以自己去探索,我的讲解到此结束,拜了个拜~~